Chemical Kinetics 12th

CLICK

 Students will be able to understand the rate of chemical reaction, Temperature dependence on the rate of reaction, Arrhenius equation and collision theory of chemical reaction. The chapter given here is to assist the students to understand the lesson in an easy and interesting way. The class 12 Chemistry Chapter 4 solutions are created by subject experts as per the latest CBSE syllabus (2020-21). Students must practise the solutions regularly to prepare effectively for their examinations.

Class 12 NCERT Solutions for Chemical Kinetics

Chemical Kinetics is a branch of chemistry. It deals with the rate of chemical reaction, the factors affecting it, the mechanism of the reaction. Based on the rate of reaction we have 3 types: Instantaneous reactions, Slow reactions and moderately slow reactions. Any chemical reaction that completes in less than 1ps time is called a fast reaction. Any chemical reaction happening for some minutes to some years is called a slow reaction. Intermediate chemical reactions that occur between fast and slow chemical reactions are called moderately slow reactions. This was a brief on Chemical Kinetics.

Subtopics for Class 12 Chemistry Chapter 4 – Chemical Kinetics

1. The rate of a Chemical Reaction
2. Factors Influencing the Rate of a Reaction
   1. Dependence of Rate on Concentration
   2. Rate Expression and Rate Constant
   3. Order of a Reaction
   4. Molecularity of a Reaction
3. Integrated Rate Equations
   1. Zero Order Reactions
   2. First-Order Reactions
   3. Half-Life of a Reaction
4. Pseudo First Order Reaction
5. Temperature Dependence of the Rate of a Reaction
   1. Effect of Catalyst Ex 4.6 – Collision Theory of Chemical Reactions.

Class 12 Chemistry NCERT Solutions (Chemical Kinetics) – Important Questions

Q 1. From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.

(a) $3\; NO(g) \rightarrow N_{2}O (g) \; Rate = k\left [ NO \right ]^{2}$

(b) $H_{2} O_{2} (aq) + 3I^{-}(aq) + 2H^{+} \rightarrow 2H_{2}O (I) + I^{-} \; Rate = k \left [ H^{2}O^{2} \right ]\left [ I^{-} \right ]$

(c) $CH_{3}CHO (g) \rightarrow CH_{4} (g) + CO (g) \; Rate = k\left [ CH_{3} CHO \right ]^{\frac{3}{2}}$

(d) $C_{2}H_{5}Cl (g) \rightarrow C_{2}H_{4} (g) + HCl (g) \; Rate = k\left [ C_{2} H_{5}Cl \right ]$

Ans:

(a) Given rate = $k\left [ NO \right ]^{2}$

Therefore, order of the reaction = 2

Dimensions of $k = \frac{Rate}{\left [ NO \right ]^{2}}$$\\ = \frac{mol \; L^{-1} s^{-1}}{\left ( mol \; L^{-1} \right )^{2}} \\ \\ = \frac{mol \; L^{-1} s^{-1}}{mol^{2}\; L^{-2}} \\ \\ = L \; mol^{-1} s^{-1}$

(b) Given rate = $k[ H_{2}O_{2} ][ I ^{-}]$

Therefore, order of the reaction = 2

Dimensions of  $k = \frac{Rate}{\left [ H_{2}O_{2} \right ]\left [ I^{-} \right ]}$$\\ = \frac{mol \; L^{-1} S^{-1}}{\left ( mol \; L^{-1} \right ) \left ( mol \; L^{-1} \right )} \\ \\ = L \; mol^{-1} s^{-1}$

(c) Given rate = $= k \left [ CH_{3} CHO \right ]^{\frac{3}{2}}$

Therefore, the order of reaction = $\frac{3}{2}$

Dimensions of $k = \frac{Rate}{\left [ CH_{3} CHO \right ]^{\frac{3}{2}}} \\ \\ = \frac{mol \; L^{-1}s^{-1}}{\left (mol \; L^{-1} \right )^{\frac{3}{2}}} \\ \\ = \frac {mol\; L^{-1} s^{-1}}{mol^{\frac{3}{2}}\; L^{\frac{3}{2}}} \\ \\ L^{\frac{1}{2}}\; mol^{ -\frac{1}{2}} \; s^{-1}$

(d) Given rate = $k = \left [ C_{2}H_{5}Cl \right ]$

Therefore, order of the reaction = 1

Dimension of $k = \frac{Rate}{\left [ C_{2}H_{5}Cl \right ]} \\ \\ = \frac{mol\; L^{-1} s^{-1}}{mol \; L^{-1}} \\ \\ = s^{-1}$

Q 2.  For the reaction: $2A + B \rightarrow A_{2}B$ is $k\left [ A \right ]\left [ B \right ]^{2}$ with $k = 2.0 \times 10^{-6}\; mol^{-2}L^{2} \; s^{-1}$. Calculate the initial rate of the reaction when [A] = 0.1 mol L–1, [B] = 0.2 mol L–1. Calculate the rate of reaction after [A] is reduced to 0.06 mol L–1

Ans:

The initial rate of reaction is

Rate = $k\left [ A \right ]\left [ B \right ]^{2} \\ \\ = \left ( 2.0 \times 10^{-6} mol^{-2} L^{2} s^{-1} \right )\left ( 0.1 \; mol \; L^{-1} \right )\left ( 0.2 \; mol \; L^{-1} \right )^{2} \\ \\ = 8.0 \times 10^{-9} mol^{-2}L^{2} s^{-1}$

When [A] is reduced from $0.1 \; mol\; L^{-1} \; to \; 0.06 \; mol\; L^{-1}$, the concentration of A reacted = $\left (0.1 – 0.06 \right ) \; mol\; L^{-1} = 0.04 \; mol\; L^{-1}$

Therefore, concentration of B reacted $= \frac {1}{2} \times 0.04 \; mol \; L^{-1} = 0.02 \; mol \; L^{-1}$

Then, concentration of B available, $\left [ B \right ] = \left ( 0.2 – 0.02 \right ) mol \; L^{-1} = 0.18\; mol \; L^{-1}$

After [A] is reduced to $0.06 \; mol \; L^{-1}$, the rate of the reaction is given by,

Rate = $k \left [ A \right ]\left [ B \right ]^{2} \\ \\ = \left ( 2.0 \times 10^{6} mol^{-2}L^{2}s^{-1} \right )\left ( 0.06\; mol L^{-1} \right )\left ( 0.18 \; mol \; L^{-1} \right )^{2} \\ \\ = 3.89\; mol \; L^{-1} s^{-1}$

Q 3. The decomposition of NH3 on platinum surface is zero order reaction. What are the rates of production of N2 and H2 if k = 2.5 × 10–4 mol–1 L s –1?

Ans:

The decomposition of NH3 on platinum surface is represented by the following equation.

$2NH^{3(g)} \overset{Pt}{\rightarrow} N_{2(g)} + 3H_{2(g)}$

Therefore,

$Rate = -\frac{1}{2}\frac{d\left [ NH_{3} \right ]}{dt} = \frac{d\left [ N_{2} \right ]}{dt} = \frac{1}{3}\frac{d\left [ H_{2} \right ]}{dt}$

However, it is given that the reaction is of zero order.

Therefore,

$-\frac{1}{2}\frac{d\left [ NH_{3} \right ]}{dt} = \frac{d\left [ N_{2} \right ]}{dt} = \frac{1}{3}\frac{d\left [ H_{2} \right ]}{dt} = k \\ \\ = 2.5 \times 10^{-4}\; mol L^{-1} s^{-1}$

Therefore, the rate of production of $N_{2}$ is

$\frac{d\left [N_{2} \right ]}{dt} = 2.5 \times 10^{-4} mol\;L^{-1}s^{-1}$

And, the rate of production of $H_{2}$  is

$\frac{d\left [H_{2} \right ]}{dt} = 3 \times 2.5 \times 10^{-4} mol\;L^{-1}s^{-1} \\ \\ = 7.5 \times 10^{-4} \; mol \;L^{-1}s^{-1}$

Q 4.  The decomposition of dimethyl ether leads to the formation of $CH_{4}, H_{2}, \; and \; CO$ and the reaction rate is given by $Rate = k\left [ CH_{3} O\, C\! H_{3} \right ]^{\frac{3}{2}}$

The rate of reaction is followed by an increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e.,

$Rate = k\left ( P_{CH_{3} O\, C\! H_{3}} \right )^{\frac{3}{2}}$

If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?

The decomposition of dimethyl ether leads to the formation of CH4, H2 and CO and the reaction rate is given by Rate = k [CH3OCH3] 3/2 The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, Rate = k p(CH OCH3 )3/2. If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?

Ans:

If pressure is measured in bar and time in minutes, then

Unit of rate = $bas \; min^{-1}$ $Rate = k\left ( P_{CH_{3} O\, C\! H_{3}} \right )^{\frac{3}{2}} \\ \\ \Rightarrow k = \frac{Rate}{k\left ( P_{CH_{3} O\, C\! H_{3}} \right )^{\frac{3}{2}}}$

Therefore, unit of rate constants  $(k) = \frac{bar\; min^{-1}}{bar^{\frac{3}{2}}} \\ \\ = bar^{\frac{-1}{2}}min^{-1}$

Q 5. Mention the factors that affect the rate of a chemical reaction.

Ans:

The factors which are responsible for the effect in chemical reaction’s rate are:

(a) Temperature

(b) Presence of a catalyst

(c) The concentration of reactants (pressure in case of gases)

Q 6. A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is (i) doubled (ii) reduced to half ?

Ans:

Let the concentration of the reactant be [A] = a

Rate of reaction, $R = k [A]^{2}\\ \\ = ka^{2}$

(a) If the concentration of the reactant is doubled, i.e [A] = 2a, then the rate if the reaction would be

$R’ = k\left ( A \right )^{2} \\ \\ = 4 ka^{2} \\ \\ = 4 \; R$

Therefore, the rate of the reaction now will be 4 times the original rate.

(b) If the concentration of the reactant is reduced to half, i.e $\left [ A \right ] = \frac{1}{2}a$, then the rate of the reaction would be

$R” = k\left ( \frac{1}{2} a \right )^{2} \\ \\ = \frac{1}{4} k a \\ \\ = \frac{1}{4} R$

Therefore, the rate of the reaction will be reduced to $\frac{1}{4} ^{th}$

Q 7. What is the effect of temperature on the rate constant of a reaction? How can this effect of temperature on rate constant be represented quantitatively?

Ans:

When a temperature of $10^{ \circ }$ rises for a chemical reaction then the rate constant increases and becomes near to double of its original value.

The temperature effect on the rate constant can be represented quantitatively by Arrhenius equation,

$k = Ae^{ -E_{a} / RT}$

Where,

k = rate constant,

A = Frequency factor / Arrhenius factor,

R = gas constant

T = temperature

$E_{a}$ = activation energy for the reaction.

Q 8. In a pseudo-first-order reaction in water, the following results were obtained:

t/s	0	30	60	90
[Ester]mol / L	0.55	0.31	0.17	0.085

Calculate the average rate of reaction between the time interval 30 to 60 seconds.

Ans:

(a) Avg rate of reaction between the time intervals, 30 to 60 seconds,

$= \frac{d\left [ Ester \right ]}{dt} \\ \\ = \frac{0.31 – 0.17}{60 – 30} \\ \\ = \frac{0.14}{30} \\ \\ = 4.67 \times 10^{-3}\; mol \; l^{-1}\; s^{-1}$

(b) For a pseudo first order reaction,

$\\k = \frac{2.303}{t} \log \frac{\left [ R \right ]_{0}}{\left [ R \right ]}\\ \\ For \; t = 30\; s \\ \\ k_{1} = \frac{2.303}{30} \log \frac{ 0.55}{ 0.31} \\ \\ = 1.911 \times 10^{-2} s^{-1} \\ \\ For \; t = 60\; s \\ \\ k_{2} = \frac{2.303}{60} \log \frac{ 0.55}{ 0.17} \\ \\ = 1.957 \times 10^{-2} s^{-1} \\ \\ For \; t = 90\; s \\ \\ k_{3} = \frac{2.303}{90} \log \frac{ 0.55}{ 0.085} \\ \\ = 2.075 \times 10^{-2} s^{-1}$

Then, avg rate constant, $k = \frac{k_{1} + k_{2} + k_{3}}{3} \\ \\ = \frac{\left (1.911 \times 10^{-2} \right ) + \left (1.957 \times 10^{-2} \right ) + \left (2.075 \times 10^{-2} \right )}{3} \\ \\ = 1.98 \times 10^{-2}\;s^{-1}$

Q 9. A reaction is first order in A and second order in B.
(i) Write the differential rate equation.
(ii) How is the rate affected on increasing the concentration of B three times?
(iii) How is the rate affected when the concentrations of both A and B are doubled?

Ans:

(a) The differential rate equation will be

$-\frac{d\left [ R \right ]}{dt} = k\left [ A \right ]\left [ B \right ]^{2}$

(b) If the concentration of B is increased three times, then

$-\frac{d\left [ R \right ]}{dt} = k\left [ A \right ]\left [ 3B \right ]^{2} \\ \\ = 9. k\left [ A \right ]\left [ B \right ]^{2}$

Therefore, the reaction rat will be increased by 9 times.

(c) When the concentrations of both A and B are doubled,

$-\frac{d\left [ R \right ]}{dt} = k\left [ 2 \right ]\left [ 2B \right ]^{2} \\ \\ = 8. k\left [ A \right ]\left [ B \right ]^{2}$

Therefore, the rate of reaction will increase 8 times.

Q10.  In a reaction between A and B, the initial rate of reaction (r0) was measured for different initial concentrations of A and B as given below:

$A/mol\; L^{-1}$	0.20	0.20	0.40
$B/mol\; L^{-1}$	0.30	0.10	0.05
$r_{0}/mol\; L^{-1}\; s^{-1}$	$5.07 \times 10^{-5}$	$5.07 \times 10^{-5}$	$1.43 \times 10^{-4}$

What is the order of the reaction with respect to A and B?

Ans:

Let the order of the reaction with respect to A be x and with respect to B be y.

Then,

$r_{0} = k\left [ A \right ]^{x} \left [ B \right ]^{y} \\ \\ 5.07 \times 10^{-5} = k\left [ 0.20 \right ]^{x}\left [ 0.30 \right ]^{y} \;\;\;\; (i) \\ \\ 5.07 \times 10^{-5} = k\left [ 0.20 \right ]^{x}\left [ 0.10 \right ]^{y} \;\;\;\; (ii) \\ \\ 1.43 \times 10^{-4} = k\left [ 0.40 \right ]^{x}\left [ 0.05 \right ]^{y} \;\;\;\; (iii)$

Dividing equation (i) by (ii), we get

$\frac{5.07 \times 10^{-5} }{5.07 \times 10^{-5} } = \frac{k\left [ 0.20 \right ]^{x}\left [ 0.30 \right ]^{y} }{k\left [ 0.20 \right ]^{x}\left [ 0.10 \right ]^{y} } \\ \\ \Rightarrow 1 = \frac{\left [ 0.30 \right ]^{y}}{\left [ 0.10 \right ]^{y}} \\ \\ \Rightarrow \left ( \frac{0.30}{0.10} \right )^{0} = \left ( \frac{0.30}{0.10} \right )^{y} \\ \\ \Rightarrow y = 0$

Dividing equation (iii) by (ii), we get

$\frac{1.43 \times 10^{-4}}{5.07 \times 10^{-5}} = \frac{k\left [ 0.40 \right ]^{x}\left [ 0.05 \right ]^{y}}{k\left [ 0.20 \right ]^{x}\left [ 0.30 \right ]^{y}} \\ \\ \Rightarrow \frac{1.43 \times 10^{-4}}{5.07 \times 10^{-5}} = \frac{\left [ 0.40 \right ]^{x}}{\left [ 0.20 \right ]^{x}} \;\;\;\;\; \begin{bmatrix} Since\; y = 0,\\ \left [ 0.05 \right ]^{y} = \left [ 0.30 \right ]^{y} = 1 \end{bmatrix} \\ \\ \Rightarrow 2.821 = 2^{x} \\ \\ \Rightarrow \log 2.821 = x \log 2 \;\;\;\;\; (taking\; log \; on \; both\; sides) \\ \\ \Rightarrow x = \frac{\log 2.821}{\log 2} \\ \\ = 1.496 \\ \\ = 1.5 \; (Approximately)$

Hence, the order of the reaction with respect to A is 1.5 and with respect to B is zero.

Q 11. The following results have been obtained during the kinetic studies of the reaction:
2A + B → C + D    

Exp.	$\frac{A}{mol L^{-1}}$	$\frac{B}{mol L^{-1}}$	Initial rate of formation of $\frac{D}{mol\; L^{-1} \;min^{-1}}$
1	0.1	0.1	$6.0 \times 10^{-3}$
2	0.3	0.2	$7.2 \times 10^{-2}$
3	0.3	0.4	$2.88 \times 10^{-1}$
4	0.4	0.1	$2.4 \times 10^{-2}$

Determine the rate law and the rate constant for the reaction.

Ans:

Let the order of the reaction with respect to A be x and with respect to B be y.

Therefore, rate of the reaction is given by,

Rate = $k\left [ A \right ]^{x} \left [ B \right ]^{y}$

According to the question,

$6.0 \times 10^{-3} = k\left [ 0.1 \right ]^{x} \left [ 0.1 \right ]^{y}$——- (1)

$7.2 \times 10^{-2} = k\left [ 0.3 \right ]^{x} \left [ 0.2 \right ]^{y}$——–(2)

$2.88 \times 10^{-1} = k\left [ 0.3 \right ]^{x} \left [ 0.4 \right ]^{y}$——–(3)

$2.4 \times 10^{-2} = k\left [ 0.4 \right ]^{x} \left [ 0.1 \right ]^{y}$——–(4)

Dividing equation (4) by (1), we get

$\frac{2.4 \times 10^{-2}}{6.0 \times 10^{-3}} = \frac{k\left [ 0.4 \right ]^{x} \left [ 0.1 \right ]^{y}}{k\left [ 0.1 \right ]^{x} \left [ 0.1 \right ]^{y}}$ $4 = \frac{\left [ 0.4 \right ]^{x}}{\left [ 0.1 \right ]^{x}}$ $4 = \left (\frac{0.4}{0.1 } \right )^{x}$ $\left (4 \right )^{1} = \left (4 \right )^{x}$

x = 1

Dividing equation (3) by (2), we get

$\frac{2.88 \times 10^{-1}}{7.2 \times 10^{-2}} = \frac{k\left [ 0.3 \right ]^{x} \left [ 0.4 \right ]^{y}}{k\left [ 0.3 \right ]^{x} \left [ 0.2 \right ]^{y}}$ $4 = \left (\frac{0.4}{0.2} \right )^{y}$ $4 = 2^{y}$ $2^{2} = 2^{y}$

y = 2

Hence, the rate law is

Rate = $k \left [ A \right ] \left [ B \right ]^{2}$

 

$k = \frac{Rate}{\left [ A \right ] \left [ B \right ]^{2}}$

From experiment 1, we get

$k = \frac{6.0 \times 10^{-3} mol\; L^{-1} \;min^{-1}}{\left (0.1 \;mol \;L^{-1} \right ) \left (0.1 \;mol \;L^{-1} \right )^{2}}$

= 6.0 $L^{2} \;mol^{-2} \;min^{-1}$

From experiment 2, we get

$k = \frac{7.2 \times 10^{-2} mol\; L^{-1} \;min^{-1}}{\left (0.3 \;mol \;L^{-1} \right ) \left (0.2 \;mol \;L^{-1} \right )^{2}}$

= 6.0 $L^{2} \;mol^{-2} \;min^{-1}$

From experiment 1, we get

$k = \frac{2.88 \times 10^{-1} mol\; L^{-1} \;min^{-1}}{\left (0.3 \;mol \;L^{-1} \right ) \left (0.4 \;mol \;L^{-1} \right )^{2}}$

= 6.0 $L^{2} \;mol^{-2} \;min^{-1}$

From experiment 1, we get

$k = \frac{2.4 \times 10^{-2} mol\; L^{-1} \;min^{-1}}{\left (0.4 \;mol \;L^{-1} \right ) \left (0.1 \;mol \;L^{-1} \right )^{2}}$

= 6.0 $L^{2} \;mol^{-2} \;min^{-1}$

Thus, rate constant, k = 6.0 $L^{2} \;mol^{-2} \;min^{-1}$

Q 12. The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table:

Exp.	$\frac{A}{mol L^{-1}}$	$\frac{B}{mol L^{-1}}$	Initial rate $mol\; L^{-1} \;min^{-1}$
1	0.1	0.1	$2.0 \times 10^{-2}$
2	—	0.2	$4.0 \times 10^{-2}$
3	0.4	0.4	—
4	—	0.2	$2.0 \times 10^{-2}$

Ans:

The given reaction is of the first order with respect to A and of zero-order with respect to B.

Thus, the rate of the reaction is given by,

Rate = $k \left [ A \right ]^{1} \left [ B \right ]^{0}$

Rate = $k \left [ A \right ]$

From experiment 1, we get

$2.0 \times 10^{-2}\, mol\; L^{-1} min^{-1} = k\left ( 0.1 \; mol \; L^{-1} \right ) \\ \\ \Rightarrow k = 0.2\; min^{-1}$

From experiment 2, we get

$4.0 \times 10^{-2}\, mol\; L^{-1} min^{-1} = 0.2 min^{-1} \left [ A \right ] \\ \\ \Rightarrow \left [ A \right ] = 0.2\; mol\; L^{-1}$

From experiment 3, we get

Rate = $0.2 \; min^{-1} \times 0.4 \; mol \; L^{-1}\\ \\ = 0.08\; mol\; L^{-1}min^{-1}$

From experiment 4, we get

$2.0 \times 10^{-2}\; mol \; L^{-1} min^{-1} = 0.2\; min^{-1} \left [ A \right ] \\ \\ \Rightarrow \left [ A \right ] = 0.1\; mol \; L^{-1}$

Q 13. Calculate the half-life of a first order reaction from their rate constants given below:

(a) $200 \; s^{-1}$

(b) $2 \; min^{-1}$

(c) $4 \; years^{-1}$

Ans:

(a) Half life, $t_{ \frac{1}{2}} = \frac{0.693}{k} \\ \\ = \frac {0.693}{200\; s^{-1}} \\ \\ = 3.47\; s$  (Approximately)

(b) $t_{ \frac{1}{2}} = \frac{0.693}{k} \\ \\ = \frac {0.693}{2\; min^{-1}} \\ \\ = 0.35\; min$  (Approximately)

(c) $t_{ \frac{1}{2}} = \frac{0.693}{k} \\ \\ = \frac {0.693}{4\; years^{-1}} \\ \\ = 0.173\; years$   (Approximately)

Q 14. The half-life for radioactive decay of 14C is 5730 years. An archaeological artifact containing wood had only 80% of the 14C found in a living tree. Estimate the age of the sample.

Ans:

Here, $k = \frac{0.693}{t_{\frac{1}{2}}} \\ \\ = \frac{0.693}{5730}years^{-1}$

It is known that,

$t = \frac{2.303}{k} \log \frac{\left [ R \right ]_{0}}{\left [ R \right ]} \\ \\ = \frac{2.303}{0.693} \log \frac{100}{80} \\ \\ = 1845\; years$      (approximately)

Hence, the age of the sample is 1845 years.

Q 15. The experimental data for decomposition of $N_{2} O_{5}$

$\left [2N_{2}O_{5} \rightarrow 4NO_{2} + O_{2} \right ]$

in gas phase at 318K are given below:

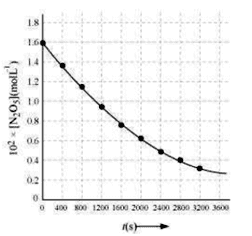
T(s)	0	400	800	1200	1600	2000	2400	2800	3200
$10^{2} \times \left [N_{2} O_{5} \right ] mol \; L^{-1}$	1.63	1.36	1.14	0.93	0.78	0.64	0.53	0.43	0.35

(a) Plot [N2O5] against t.
(b) Find the half-life period for the reaction.
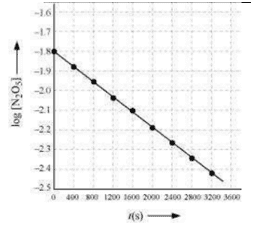
(c) Draw a graph between log[N2O5] and t.
(d) What is the rate law?

(e) Calculate the rate constant.
(f) Calculate the half-life period from k and compare it with (b).

Ans:

(a)

(b) Time corresponding to the concentration, $\frac{1.630 \times 10^{2}}{2}\; mol\; L^{-1} = 81.5 mol\; L^{-1}$ is the half-life. From the graph, the half-life obtained as 1450 s.

(c)

t(s)	$10^{2} \times \left [N_{2} O_{5} \right ] mol \; L^{-1}$	$\log \left [ N_2 O_{5} \right ]$
0	1.63	-1.79
400	1.36	-1.87
800	1.14	-1.94
1200	0.93	-2.03
1600	0.78	-2.11
2000	0.64	-2.19
2400	0.53	-2.28
2800	0.43	-2.37
3200	0.35	-2.46

(d) The given reaction is of the first order as the plot, $\log \left [ N_2 O_{5} \right ]$ v/s t, is a straight line.

Therefore, the rate law of the reaction is

Rate = $k \left [ N_2 O_{5} \right ]$

(e) From the plot, $\log \left [ N_2 O_{5} \right ]$ v/s t, we obtain

$Slope = \frac{-2.46 – \left ( -1.79 \right )}{3200 – 0} \\ \\ = \frac{-0.67}{3200}$

Again, slope of the line of the plot $\log \left [ N_2 O_{5} \right ]$ v/s t is given by

$- \frac{k}{2.303}$.

Therefore, we obtain,

$- \frac{k}{2.303} = – \frac{0.67}{3200} \\ \\ \Rightarrow k = 4.82 \times 10^{-4}s^{-1}$

(f) Half – life is given by,

$t_{\frac{1}{2}} = \frac{0.639}{k} \\ \\ = \frac{0.693}{4.82 \times 10^{-4}}S \\ \\ = \frac{1.483}{10^{3}}s \\ \\ = 1438 s$

This value, 1438 s, is very close to the value that was obtained from the graph.

Q 16. The rate constant for a first-order reaction is 60 s–1. How much time will it take to reduce the initial concentration of the reactant to its 1/16th value?

Ans:

It is known that,

$t = \frac{2.303}{k} \log \frac{\left [ R \right ]_{0}}{\left [ R \right ]} \\ \\ = \frac{2.303}{60\; s^{-1}} \log \frac{1}{1/6} \\ \\ = \frac{2.303}{60\; s^{-1}} \log 16 \\ \\ = 4.6 \times 10^{-2} \left ( approximately \right )$

Hence, the required time is $4.6 \times 10^{-2}\; s$.

Q 17. During the nuclear explosion, one of the products is 90Sr with a half-life of 28.1 years. If 1µg of 90Sr was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically.

Ans:

$k = \frac{0.693}{t_{\frac{1}{2}}} = \frac{0.693}{28.1}\; y^{-1}$

Here,

It is known that,

$t = \frac{2.303}{k} \log \frac{\left [ R \right ]_{0}}{\left [ R \right ]} \\ \\ \Rightarrow 10 = \frac{2.303}{\frac{0.693}{28.1}} \log \frac{1}{\left [ R \right ]} \\ \\ \Rightarrow 10 = \frac{2.303}{\frac{0.693}{28.1}}\left ( – \log \left [ R \right ] \right ) \\ \\ \Rightarrow \log \left [ R \right ] = – \frac{10 \times 0.693}{2.303 \times 28.1}\\ \\ \Rightarrow \left [ R \right ] = antilog \left ( – 0.1071 \right )\\ \\ = antiog \left ( 1.8929 \right ) \\ \\ = 0.7814 \mu g$

Therefore, $0.7814 \; \mu g$ of $^{90}Sr$ will remain after 10 years.

Again,

$t = \frac{2.303}{k} \;log \frac{\left [ R \right ]_{0}}{\left [ R \right ]} \\ \\ \Rightarrow 60 = \frac{2.303}{\frac{0.693}{28.1}} \log \frac{1}{\left [ R \right ]}\\ \\ \Rightarrow log \left [ R \right ] = – \frac{60 \times 0.693}{2.303 \times 28.1}\\ \\ \left [ R \right ] = antilog \; \left ( – 0.6425 \right ) \\ \\ = antilog \left ( 1.3575 \right )\\ \\ = 0.2278 \mu g$

Therefore, $0.2278 \mu g \; o\!f \; ^{90}Sr$ will remain after 60 years.

Q 18. For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction.

Ans:

For a first order reaction, the time required for 99% completion is

$t_{1} = \frac{2.303}{k} \log \frac{100}{100 – 99} \\ \\ = \frac{2.303}{k} \log 100 \\ \\ = 2 \times \frac{2.303}{k}$

For a first order reaction, the time required for 90% completion is

$t_{1} = \frac{2.303}{k} \log \frac{100}{100 – 90} \\ \\ = \frac{2.303}{k} \log 10 \\ \\ = \frac{2.303}{k}$

Therefore, $t_{1} = 2 \; t_{2}$

Hence, the time required for 99% completion of a first order reaction is twice the time required for the completion of 90% of the reaction.

Q 19. A first-order reaction takes 40 min for 30% decomposition. Calculate t1/2.

Ans:

For a first order reaction,

$t = \frac{2.303}{k} \log \frac{\left [ R \right ]_{0}}{\left [ R \right ]} \\ \\ k = \frac{2.303}{40\; min} \log \frac{100}{100 – 30} \\ \\ = \frac{2.303}{40 \; min} \log \frac{10}{7} \\ \\ = 8.918 \times 10^{-3} \; min^{-1}$

Therefore,